| .: навигация :. |
 |
| На главную |
| О сайте |
| Ссылки |
| Настройки |
| Контакты |
| Помощь |
 |
 |
| .: астрология :. |
 |
 |
| Текущее |
| Натальная карта |
| Транзиты |
| Соляр |
| Синастрия |
| Прогрессии |
| Диспозиторы |
| Дирекции |
 |
 |
 |
 |
| .: биоритмология :. |
 |
 |
| Биоритмы |
| Прогноз на год |
| Магнитные бури |
| Давление |
 |
 |
| .: исследования :. |
 |
 |
| LiveJournal |
| База SADC |
| YouTube/Twitch |
| Earthquakes |
| Браки и разводы |
| Фрилансеры |
 |
 |
| .: эксперименты :. |
 |
 |
| Аспекты профессий |
| Астроблизнецы |
 |
 |
| .: таблицы и справочники :. |
 |
 |
| Справочник аспектов |
| Ретроградный Меркурий |
| Лунный календарь |
| Благоприятные дни |
 |
 |
| .: психология :. |
 |
 |
| Психологический тест |
 |
 |
| .: таро :. |
 |
 |
| Карты Таро |
Исследование Youtube/Twitch
Самый быстрый способ научиться различать знаки зодиака - непосредственное наблюдение за их деятельностью.
Используя всю мощь сообщества любителей астрологии на сайте запущен проект по исследованию видеоблоггеров.
Если вы смотрите YouTube канал или Twitch стрим популярного видеоблоггера и дата его рождения общеизвестна - сообщите эту информацию. Полученные данные будут собираться на спец. сайте. Фазы исследования: 1. Сбор статистики 2. Корректировка и анализ 3. Выводы
Ход исследования:
1. Сбор данных В ходе сбора статистики выяснилось, что влоггеров миллионников огромное множество, в выборку попала лишь малая часть: США, Россия, Венесуэла, Испания, Великобритания. По каждому знаку было добавлено по 50 влоггеров имеющих более 1 млн. подписчиков. 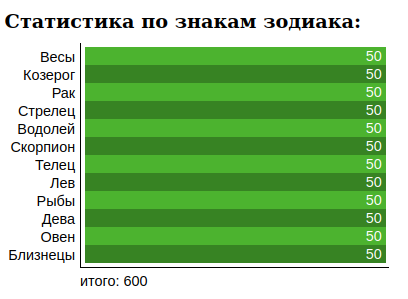 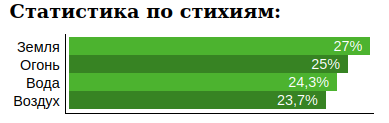 2-4. Подсчет аспектов / генерация случайных дат рождений
Комментарий к таблице:
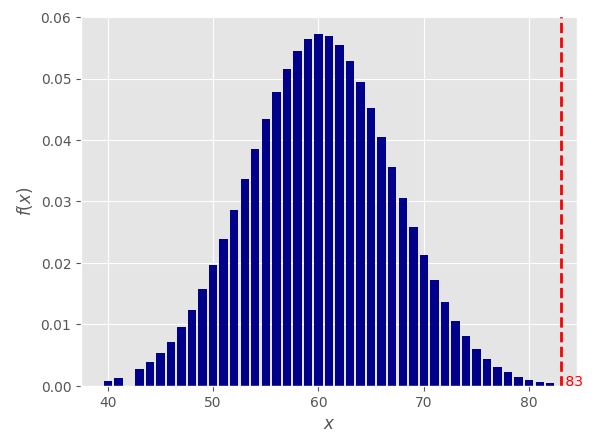
5. Поиск отклонений (расчет вероятности) Расчет вероятности осуществляется стандартными методами для нормального распределения. Для нашего примера из таблицы: имеем величины: 57,56,57,59,62,58,59,73 вычисляем среднее значение (мат. ожидание): 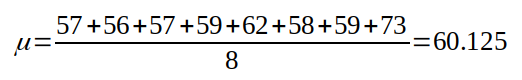 вычисляем среднее арифметическое квадратов отклонений (дисперсию): 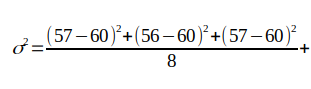 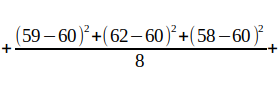 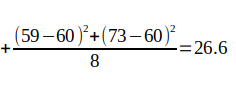 берем корень и получаем стандартное отклонение (сигма): 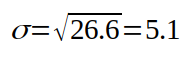 теперь мы можем посчитать вероятность получения указанного количества аспектов по формуле Лапласа: 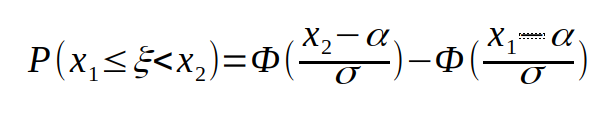 Например, какая вероятность, что искомое значение (сумма аспектов "Квадратура Марс-Плутон (угловое расстояние между Марсом и Плутоном 90 градусов)" в датах рождения 600 влоггеров) будет находиться в диапазоне от 82 до 84? Подставляем в формулу значения: x1=82, x2=84, σ=5, α=60, получаем: 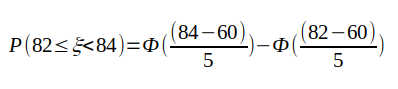  Итоговая вероятность получилась равной 0,000029 или 1 / 34482 ! Процесс вычисления вероятности можно автоматизировать с помощью простейшей программы на языке Python: # Подключаем библиотеку SciPy from scipy import stats # Задаем параметры: loc=60 - среднее значение, scale=5 - стандартное отклонение (сигма) calc = stats.norm(loc=60, scale=5) # Устанавливаем значение для которого ищется вероятность и выводим результат print(calc.pdf(83)) Вычисление среднего значения и стандартного отклонения можно так же упростить с помощью скрипта: # Подключаем библиотеку NumPy import numpy as np # Массив с данными data=[57,56,57,59,62,58,59,73] # Рассчитываем среднее (мат. ожидание) print(np.mean(data)) # Рассчитываем стандартное отклонение (сигма) print(np.std(data)) Для более равномерного распределения случайных дат рождений использовался подсчет количества аспектов "Квадратура Марс-Плутон" не в 8 случайных выборках по 600 дат, а в 1000: 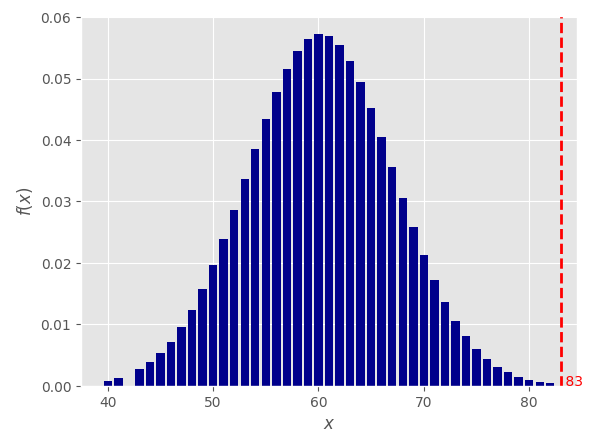 Что показывает этот график? На графике отображено насколько маловероятно получить значение 83, случайно генерируя даты рождений (число лежит практически за пределами графика - более 4-х стандартных отклонений (сигм)). Небольшое отступление: что такое нормальное распределение? Представьте, что вы бросаете два игральных кубика, каждый с шестью пронумерованными сторонами от 1 до 6. Результаты экспериментов записываете в таблицу; допустим, вы делаете 100 бросков. У вас получаются записи с номером эксперимента и результатом: 1 - 3 2 - 7 3 - 5 4 - 7 5 - 10 ... 100 - 5 Далее вы группируете выпавшие значения; какие-то значения будут выпадать чаще, какие-то реже. Если отобразить эти значения на графике, то вы увидите колоколообразный график - нормальное распределение. Для примера, как выглядит величина, которая не маловероятна -"Тригон Меркурий-Марс" (угловое расстояние между Меркурием и Марсом 120 градусов): 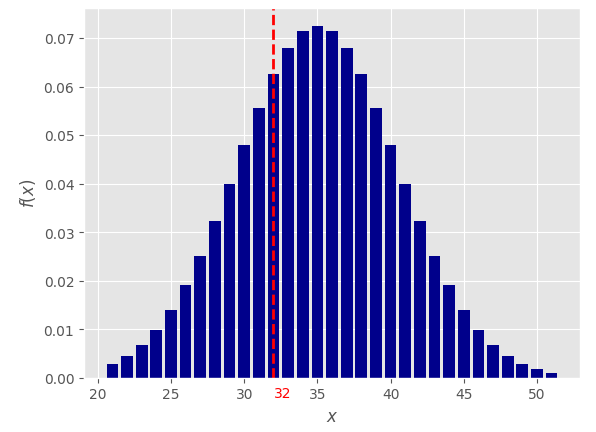 Можно подумать, что это из за того, что Меркурий -быстрая планета и это влияет на частоту выпадания аспекта, но взглянем на аспект "Секстиль Меркурий-Венера" (угловое расстояние между Меркурием и Венерой 60 градусов): 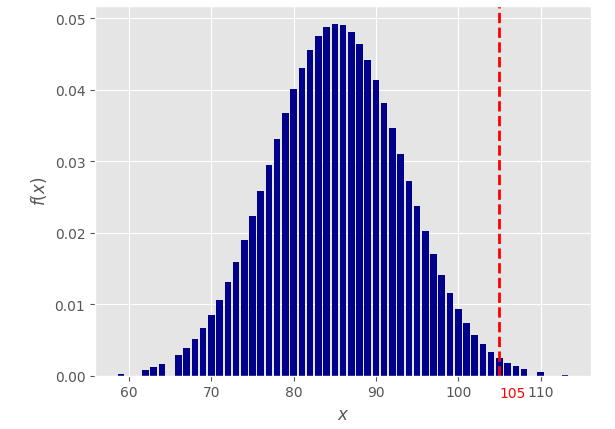 Варианты обьяснения полученных аномалий: 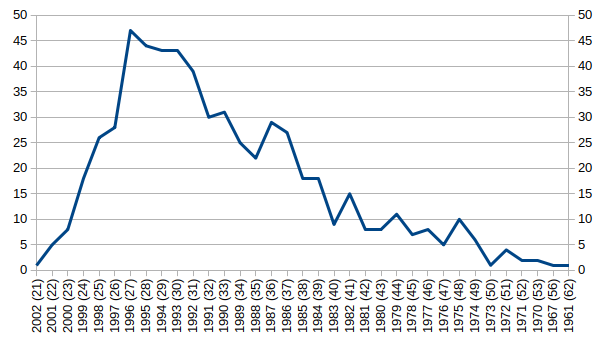
Разберем более подробней на примере аспекта "Квадратура Марс-Плутон", за счет чего произошло отклонение.
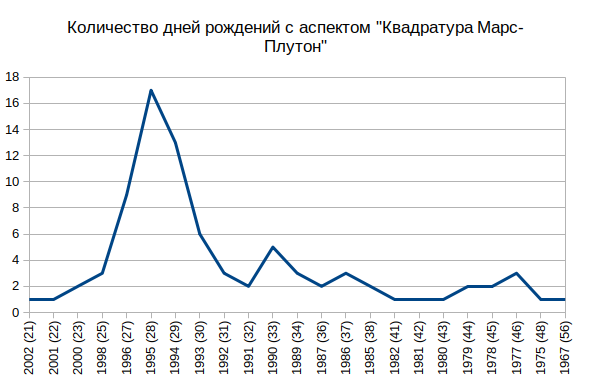 Из них 39 человек (1994-1996) родились в период 1994-2000, когда данный аспект встречался в 2-3 раза чаще чем обычно (52-82 дня в году, вместо 22-30 в другие годы): 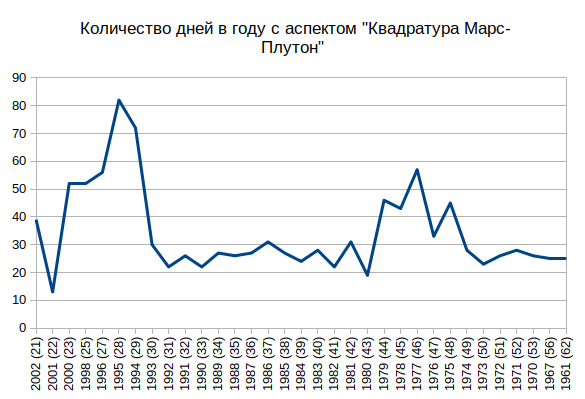 Астрологическое обьяснение: Влоггеры часто рождались в период времени, когда наблюдалась квадратура Марса к Плутону (во внимание не берется ни в каких знаках находились указанные планеты, ни возможное влияние целого комплекса аспектов или других астрологических критериев). Не астрологическое обьяснение:
Итоговая таблица по аномалиям: (вероятность расчитана для 8 выборок по 600 дат; кликните на аспект, чтобы посмотреть вероятность для 1000 выборок по 600 дат) Max - аспект встречается аномально часто. Min - аспект встречается аномально редко. вероятность 1/1000 и менее (за пределами нормального распределения):
Квадратура Марс-Плутон
вероятность для 1000 выборок: 1/3702 (0.0002701069)
Оппозиция Солнце-Уран
 вероятность для 1000 выборок: 1/487 (0.0020519080)
Оппозиция Солнце-Сатурн
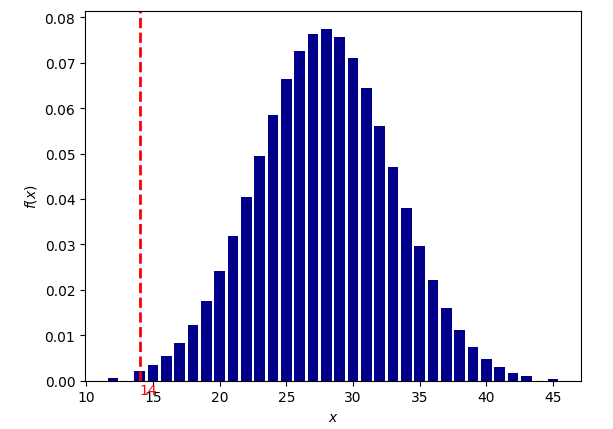 вероятность для 1000 выборок: 1/265 (0.0037621053)
Тригон Марс-Сатурн
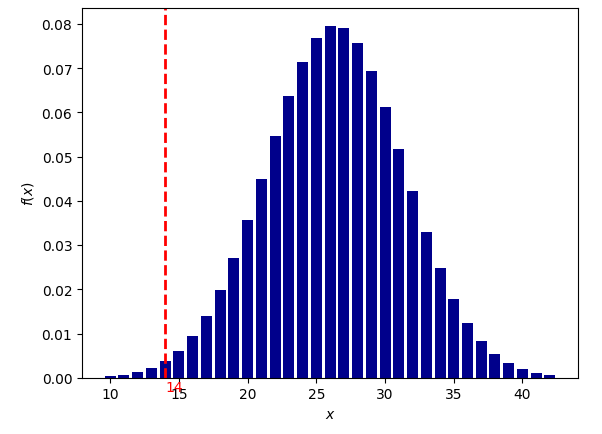 вероятность для 1000 выборок: 1/263 (0.0037968748)
Секстиль Меркурий-Венера
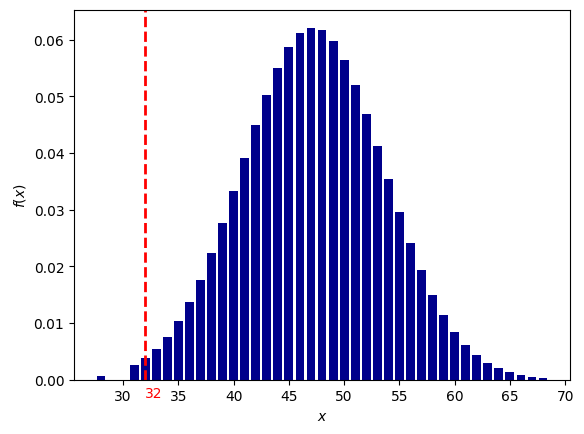 вероятность для 1000 выборок: 1/392 (0.0025449610)
Секстиль Марс-Юпитер
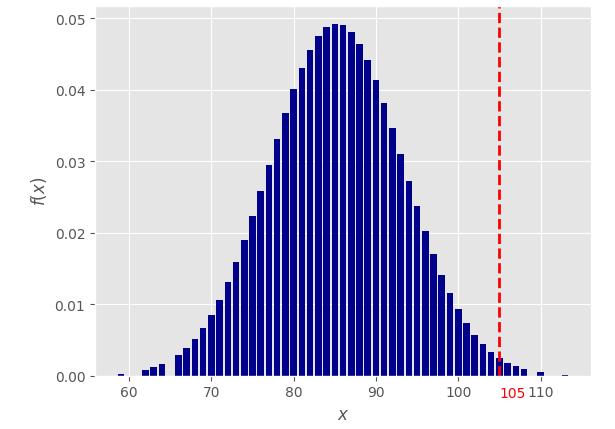 вероятность для 1000 выборок: 1/97 (0.0102597410)
Секстиль Венера-Уран
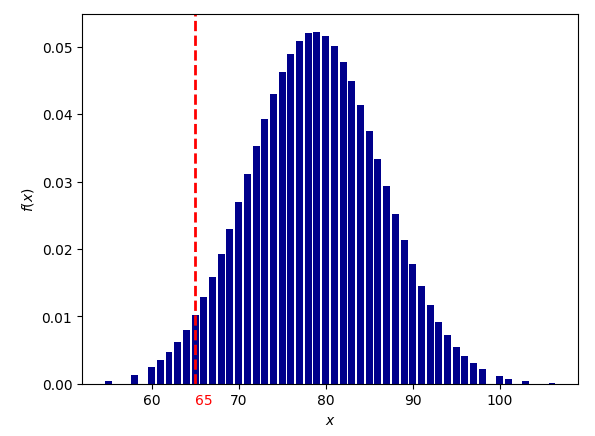 вероятность для 1000 выборок: 1/154 (0.0064577678)
Квадратура Венера-Марс
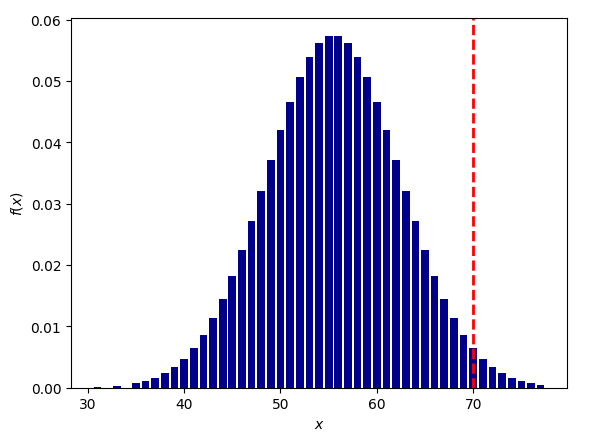 вероятность для 1000 выборок: 1/318 (0.0031364830)
Соединение Меркурий-Нептун
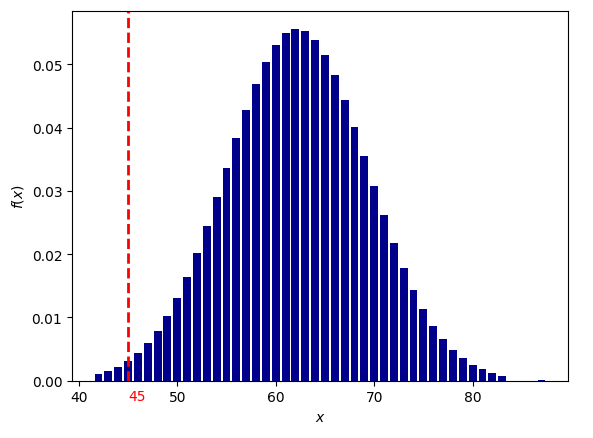 вероятность для 1000 выборок: 1/23 (0.0426045220)
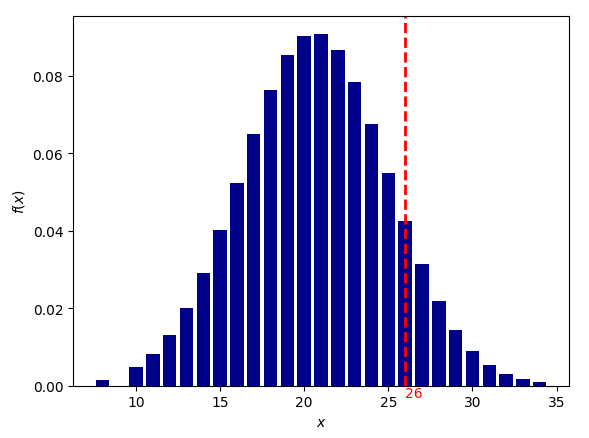 вероятность от 1/200 до 1/1000: Секстиль Меркурий-Марс вероятность для 1000 выборок: 1/103 (0.0096406470)
Секстиль Солнце-Сатурн
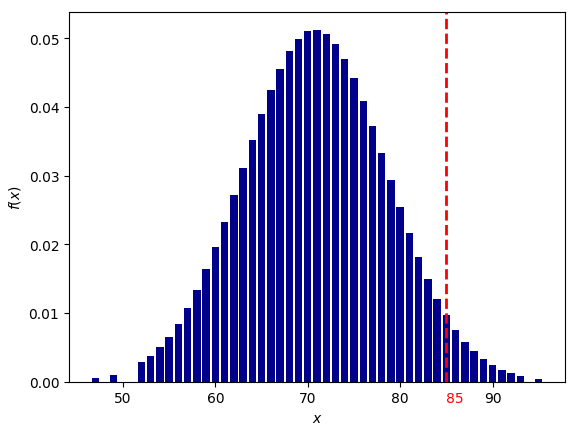 вероятность для 1000 выборок: 1/185 (0.0053960988)
Оппозиция Солнце-Юпитер
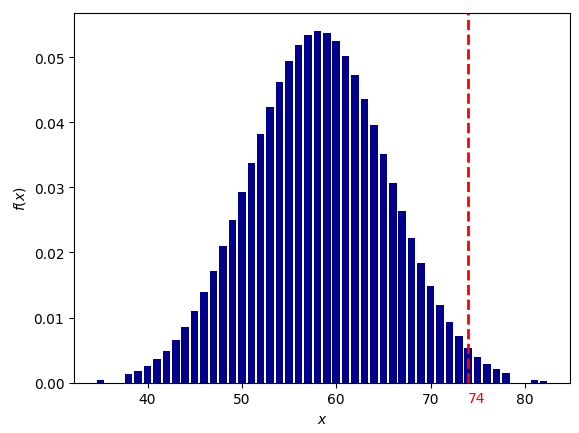 вероятность для 1000 выборок: 1/140 (0.0071204133)
Секстиль Юпитер-Уран
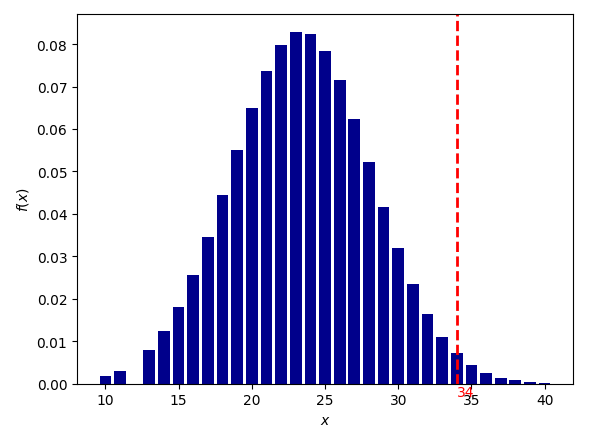 вероятность для 1000 выборок: 1/74 (0.0134865655)
Квадратура Луна-Венера
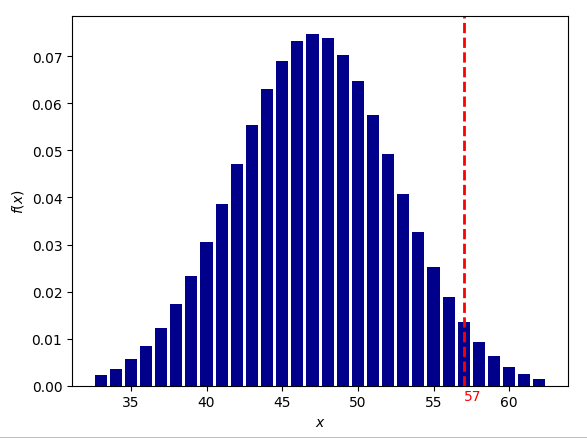 вероятность для 1000 выборок: 1/102 (0.0097982360)
Секстиль Сатурн-Нептун
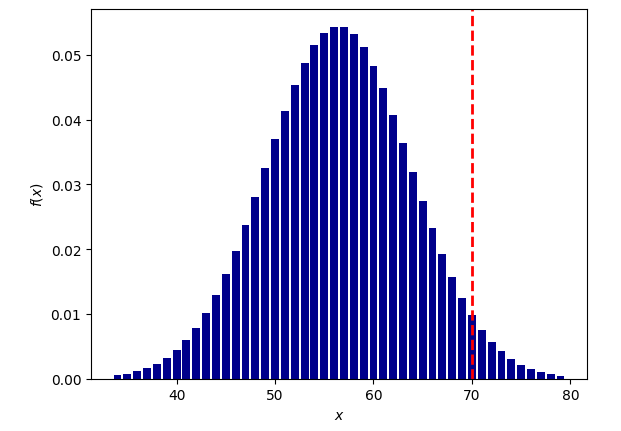 вероятность для 1000 выборок: 1/32 (0.0306059657)
Секстиль Уран-Плутон
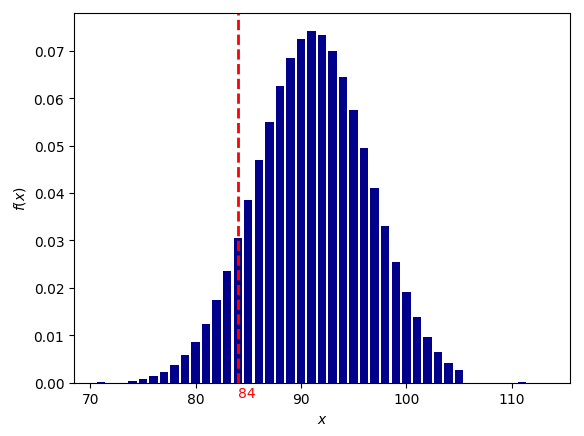 вероятность для 1000 выборок: 1/813 (0.0012290935)
Оппозиция Меркурий-Сатурн
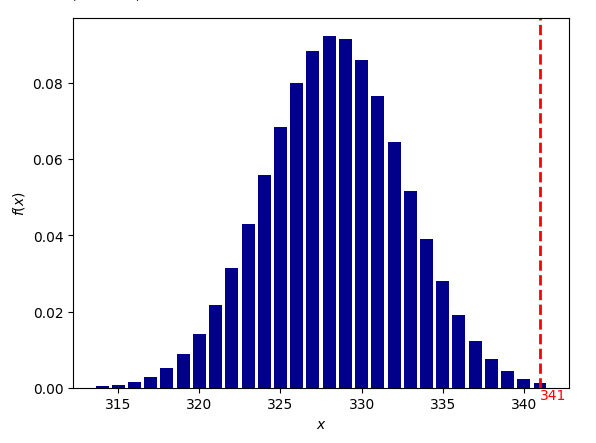 вероятность для 1000 выборок: 1/66 (0.0149475595)
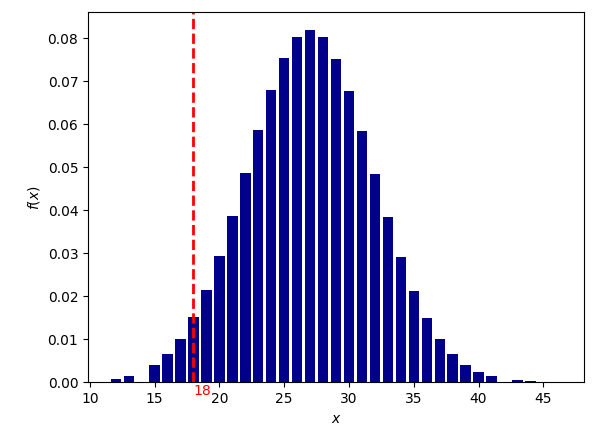 Благодарю всех, кто принял участие в эксперименте и присылал ссылки на каналы влоггеров! update: 12.02.2025 |
| .: текущее :. |
 |

|
